
(c) Nazim Fatès, Janvier 2002, pour Futura.

Qui n'a pas été un jour impressionné en voyant les " ola ", ces vagues tournantes que les supporters des clubs de foot s'amusent à faire pour encourager leurs joueurs ou pour créer le spectacle ? Supposons que vous vouliez déclencher une ola dans un stade, comment allez-vous procéder ? Allez-vous dire à chaque personne à quel moment elle doit se lever, ce n'est pas réaliste. Il est bien plus économique de dire à chaque personne d'obéir à une règle simple : " Si vous voyez l'un de vos voisins se lever, levez-vous à votre tour en agitant les bras. " Si la majorité des spectateurs est d'accord pour coopérer, il suffira qu'une poignée de meneurs amorce la vague pour que celle-ci se propage indéfiniment (ou jusqu'à fatigue des supporters) dans le stade.
Bien, grâce à vos encouragements, votre équipe de foot favorite a remporté ce match à domicile et caracole maintenant en tête du championnat. Vous rentrez chez vous et subitement, l'envie vous prend de mieux comprendre ce qui s'est déroulé au moment de la ola : vous cherchez à modéliser ce phénomène. Quel outil mathématique allez-vous choisir ? Allez vous considérer le stade comme un milieu continu et prendre une équation différentielle ordinaire ou une équation aux dérivées partielles ? C'est une possibilité, mais en oubliant qu'un stade est constitué d'individus bien séparés les uns des autres, vous risquez de passer à coté de nombreuses propriétés de la ola, notamment le fait que la vague meurt dès que le nombre de personnes prêtes à coopérer est insuffisant.
Il existe pourtant un outil tout désigné pour la modélisation des types de phénomènes dans lesquels les individus obéissent à une règle locale où l'on adapte son comportement en fonction des voisins: il s'agit des automates cellulaires. L'exposé qui suit a pour de présenter des d'un mémoire de DEA, effectué en Histoire et Philosophie des sciences à la Sorbonne sur le thème des automates cellulaires.
Les automates cellulaires ont été inventés par Stanislaw Ulam (1909-1984) et John von Neumann (1903-1957) à la fin des années 40 au Los Alamos National Laboratory (Etats-Unis).


En 1949, von Neumann donna une série de cours sur le thème : " Théorie et organisation des automates complexes " ; une des questions centrales de ce cours étant de savoir s'il était possible de concevoir une machine capable de s'auto-reproduire. En effet, il est clair que les objets fabriqués par une machine sont généralement plus simples que la machine elle-même. Prenons l'exemple d'une usine de fabrication de bouteilles de soda, on ne contestera pas dans ce cas que la bouteille est plus simple que la machine qui l'a fabriquée. Même dans le cas d'une usine de fabrication d'ordinateurs, l'outillage utilisé est bien plus complexe que le produit fabriqué.
Von Neumann émit l'idée qu'une machine capable de manipuler des composants de machine élémentaires pourrait résoudre ce problème. Dans sa première conception, l'automate devait puiser dans un réservoir de composants de machine et construire un automate similaire à lui-même, à la façon dont on construit un automate par un jeu de " Meccano ". Mais cela nécessitait que l'automate soit doté d'un système de vision et de reconnaissance suffisamment élaboré pour pouvoir distinguer les différents éléments de machine. Cet automate aurait dû être en outre doté de capacités exceptionnelles pour pouvoir souder et manipuler des tubes à vide sans les abîmer. Ces exigences étaient tout simplement inconcevables étant donné l'état des techniques dans les années 50.
La solution à ce problème vint d'un collègue de von Neumann au laboratoire de Los Alamos : Stanislaw Ulam s'intéressait aux " objets géométriques définis de façon récursive " qu'il étudiait après les heures réglementaires de travail en utilisant les ordinateurs du laboratoire de Los Alamos. Ces objets provenaient de jeux aux règles simples dans lesquels on pouvait voir des figures [patterns] se développer, se reproduire, combattre pour une portion de territoire et mourir. Ces jeux se déroulaient dans un univers " cellulaire ", composé d'une matrice infinie où les cellules, régulièrement réparties, peuvent être dans un état passif ou un état actif. Les figures de cet univers étaient composées des cellules actives, et à tout moment, le devenir de chaque cellule était dicté par l'état des cellules avoisinantes. Ulam s'aperçut que l'analyse de ces figures défiait le bon sens : elles semblaient évoluer dans un monde qui leur était propre avec des lois bien spécifiques. Il suggéra alors à von Neumann d'utiliser un tel monde abstrait pour pallier les difficultés pratiques qui se posaient pour la construction de l'automate auto-reproducteur. Ce monde serait suffisamment complexe pour pouvoir simuler les opérations élémentaires des machines et en même temps construit de façon à ce que les lois de la physique qui gouvernent ce monde se réduisent à quelques règles simples. L'idée plut à von Neumann qui était habitué à voir les machines comme des circuits logiques, il adopta donc l'univers d'Ulam pour commencer à réfléchir à son automate [Poundstone85].
Un premier problème était résolu mais il restait à concevoir un mécanisme d'auto-reproduction. Von Neumann aboutit à l'idée qu'un automate auto-reproducteur devrait comporter une unité baptisée " constructeur universel " qui serait capable de fabriquer n'importe quelle machine (cellulaire) à partir d'une description qui lui serait fournie. Dans le cas particulier où l'on fournirait la description de constructeur universel au constructeur universel lui-même, il y aurait auto-reproduction. Le raisonnement semble simple à première vue mais il se pose un problème de logique : le système auto-reproducteur (SAR) est constitué du constructeur universel (CU) et de sa propre description (DESC). Or cette description ne peut être la description du constructeur universel seulement, elle doit être la description de tout le système, et donc être en particulier une description de la description. En équations, nous avons : SAR = CU + DESC ( SAR ), ce qui paraît a priori insoluble étant donné l'existence d'une régression à l'infini (lorsqu'on remplace SAR dans le terme de droite par le contenu de l'équation).
Ce problème pouvait-il être résolu? Existait-il un moyen d' " expliquer " à l'automate que la description ne devait pas s'inclure elle-même ? Von Neumann s'inspira des travaux de Turing pour trouver un remède. Nous devons en effet à Church et à Turing l'idée selon laquelle tout calcul [Turing36], et plus généralement tout problème bien formalisé [Turing54] quel que soit sa complexité, peut être réduit à une séquence d'opérations appelée " algorithme ". Ces opérations sont choisies dans un catalogue réduit et leur exécution peut être confiée à une seule machine précise appelée machine universelle. Selon la thèse dite de Church-Turing, cette machine posséderait la capacité (virtuelle) de résoudre tout calcul, aussi complexe soit-il. Nous nommerons cette propriété la " calculabilité universelle ". Le fait que ces opérations élémentaires soient choisies dans un catalogue fini permet leur transcription dans l'univers cellulaire ou le nombre d'états des cellules est aussi fini.
Le problème fut résolu par von Neumann en ajoutant une troisième unité : une machine universelle de Turing, le superviseur, devait orchestrer le processus. L'utilisation du superviseur évitait la régression à l'infinie en distinguant deux phases :
(1) L'ensemble ( constructeur universel + superviseur ), le " copieur-superviseur " réalise une copie de lui-même dans une région vide de l'espace en lisant la description, c'est la phase d'interprétation.
(2) La phase (1) étant terminée, le superviseur comprend qu'il ne faut plus que la description soit interprétée ; celle-ci est considérée comme un ensemble de données et recopiée littéralement pour rebâtir le système initial [Heudin98].
En 1952, la description de l'automate auto-reproductif était terminée et von Neumann proposait une version qui utilise 29 types de cellules différentes. L'état de chaque cellule au temps t était déterminé uniquement par l'état des quatre cellules adjacentes et celui de la cellule centrale au temps t-1. Ce voisinage est d'ailleurs nommé voisinage de von Neumann en hommage à son inventeur. Néanmoins, même dans l'univers simplifié des automates cellulaires, l'ensemble ( constructeur universel + machine de Turing universelle + description du système ) était constitué de plus de 200 000 cellules ! Après cette première " victoire " et de façon assez surprenante, von Neumann allait délaisser l'étude des automates cellulaires pour s'atteler à d'autres problèmes scientifiques et ses résultats concernant l'auto-reproduction ne seront jamais publiés de son vivant. Il est possible que la trop grande complexité de son modèle l'ait déçu. En outre, la " physique " qui régissait ce monde artificiel possédait un défaut majeur : elle n'était pas réaliste puisqu'elle ne respectait pas les conditions de symétrie du monde physique.
Il faudra attendre, les travaux de Codd en 1968, pour voir la publication du premier manuel consacré aux automates cellulaires. Pour reprendre le vocabulaire de Kuhn dans La structure des révolutions scientifiques [Kuhn70], on peut dire que l'apparition d'un manuel ainsi que la création de problèmes qui occupent une communauté est le signe que ce domaine d'étude devient un champ théorique digne de ce nom, autrement dit qu'un paradigme est en train de naître. Il est néanmoins trop tôt pour dire qu'il existe un nouveau domaine scientifique : les automates cellulaires restent à ce stade une branche particulière ce que les historiens des sciences nomment " la première cybernétique. "
Dans le numéro d'Octobre 1970 de Scientific American, Martin Gardner publie un article intitulé " Les combinaisons fantastiques du Jeu de la Vie de John Conway " [Gardner70]. Conway a inventé un automate cellulaire qui a la particularité suivante : des figures peuvent croître et atteindre une grande taille mais pourtant, on ne peut dire de façon évidente s'il existe des figures qui vont croître à l'infini. Cet automate cellulaire se nomme 'Game of Life' ou 'Life' en abrégé.
Les règles du Jeu de la Vie sont extrêmement simples. Les cellules peuvent se trouver dans deux états qui sont : vivant / mort, l'espace cellulaire est composé de cellules qui se trouvent dans l'état mort au départ, sauf pour un nombre fini d'entre elles. L'évolution de chaque cellule est déterminée en fonction du nombre Nv de cellules vivantes se trouvant dans les huit cases adjacentes à une cellule. Les règles sont :
* Une cellule vivante meurt (devient vide) pour Nv = 1 : cela correspond à un état d'isolement de cellule.
* Une cellule vivante meurt pour Nv = 4 : cela correspond à un état de surpeuplement autour de la cellule.
* Une cellule morte peut devenir vivante pour Nv = 3 : cela correspond à une reproduction " trisexuée ".
Le Jeu de la Vie marque un tournant dans l'étude des automates cellulaires car contrairement aux modèles précédents où l'on décidait des règles et du nombre d'état dans un but bien précis (prouver la calculabilité universelle, la constructibilité universelle), on cherche désormais à trouver les propriétés des automates d'après leur règles de fonctionnement. Le travail des chercheurs s'apparente alors à celui des physiciens qui étudient des phénomènes, préparent des expériences et essaient de découvrir de nouveaux objets. Néanmoins, il existe une différence de taille avec le travail des physiciens : l'évolution des objets manipulés, bien que totalement déterminée par les fonctions de transition, est hautement imprévisible. On remarque ainsi qu'il n'y a pas de correspondance apparente entre la taille d'une configuration initiale et le temps qu'elle met pour se stabiliser. Par ailleurs, le simple fait d'ajouter ou d'enlever une cellule dans une configuration change son évolution de façon radicale. Comment, dans ces conditions, espérer parvenir à construire une expérience ?
L'étude des propriétés de Life a démarré avec celle de la découverte des objets stables. Généralement, les chercheurs classent les objets selon leur forme de stabilité. Les objets les plus simples à étudier sont ceux qui restent identiques à eux-mêmes avec le temps, un bloc carré de quatre cellules par exemple. Viennent ensuite les objets qui dont l'évolution est périodique, nommés oscillateurs. L'oscillateur le plus simple est le 'clignotant' ; il est constitué de trois cellules alignées, et possède une période 2. Une autre classe d'objets importants est celle des objets périodiques qui se translatent avec le temps. Le planeur est l'exemple le plus simple et il apparaît de façon spontanée lors des simulations.
Petit à petit, les chercheurs ont procédé comme des naturalistes et ont découvert des figures stables de plus en plus complexes. Ces découvertes se font selon deux méthodes : la première consiste à initialiser l'espace cellulaire de façon aléatoire et à observer les figures qui apparaissent de façon spontanée. La seconde méthode consiste à construire, par des procédés souvent très ingénieux, des figures périodiques qui éventuellement se translatent. Un grand concours -implicite - a débuté au début des années 70 pour la découverte de nouvelles figures stables. Les chercheurs ont rivalisé d'astuce et ont fini par mettre à jour toute une faune exotique qui peuple l'univers du Jeu de la Vie. Des noms aussi évocateurs que " le mangeur, la navette, le crapaud, le phare ou le serpent " ont été donnés (et continuent d'être données) aux figures stables découvertes. On peut dresser un parallèle avec ce qui se produit en astronomie, où les chercheurs rivalisent pour l'observation de nouveaux astres, avec à la clé la possibilité de nommer l'astre du nom du découvreur. Vu de l'extérieur, cette course folle au plus complexe semblait futile aux autres scientifiques. L'étude du Jeu de la Vie prit des proportions telles qu'en 1974, on pouvait lire dans les colonnes du magazine américain Time que " des heures de calcul représentant des millions de dollars avaient été gaspillées par la horde grandissante des fanatiques de ce jeu " [Time74].
Ce jugement sévère était-il justifié ? Ces chercheurs étaient-ils des " fanatiques " ou à l'opposé plutôt des " scientifiques " dont la discipline n'était pas encore reconnue ? La recherche des propriétés de Life peut-elle être qualifiée de " scientifique " ? Selon le scénario proposé par Kuhn, une discipline scientifique apporte des " énigmes " [puzzles] à la communauté scientifique concernée. Nous pouvons donc essayer d'estimer la 'scientificité' de l'étude du Jeu de la Vie en étudiant les " énigmes " qui sont nées de l'étude du Jeu de la Vie.
Le premier problème fut posé par Conway lui-même qui, en 1970, conjectura qu'il existait des figures (ensembles de cellules vivantes) qui pouvaient croître de façon illimitée. Conway avait créé le Jeu de la Vie en espérant qu'une telle possibilité pourrait être réalisée ; néanmoins aucune preuve mathématique de la réalisation de la croissance illimitée ne pouvait être établie. Il fallait donc exhiber une figure dont l'évolution soit totalement prévisible et dont la taille augmente de façon régulière. Gardner offrit un prix symbolique à celui qui arriverait à prouver ou à réfuter la conjecture de Conway avant la fin de l'année. Le prix fut remporté par William Gosper et cinq autres informaticiens du MIT qui réussirent à exhiber une figure, baptisée lance-planeur (" glider gun "), qui est un oscillateur à l'évolution cyclique et qui a la propriété d'émettre un planeur toute les trente générations. Une telle découverte n'aurait rien d'impressionnant de nos jours mais il faut se souvenir qu'en 1970, nous sommes à l'aube de l'ère informatique et que les simulations d'évolutions se mènent parfois à l'aide de pions de jeu de dames ou d'Othello. L'existence du " lance-planeurs " constituait la première résolution d'une énigme liée au Jeu de la Vie : elle démontrait que la croissance illimitée était possible.
Un autre problème qui a occupé la communauté des chercheurs fut celui de la réversibilité. Un automate est dit être réversible s'il ne se produit pas de perte d'information au cours de l'évolution de l'automate : chaque configuration possède donc un unique successeur (déterminisme de l'AC) et un unique prédécesseur. Il est clair que l'on peut déduire facilement des règles du Jeu de la Vie que l'on n'est pas en présence d'un automate réversible puisque des configurations différentes peuvent avoir un même successeur. Par contre, une propriété qui n'était pas évidente était l'existence de configurations qui n'admettent aucun état qui puisse les engendrer. De telles configurations sont appelées " jardins d'Eden " car elles ne peuvent être que des états initiaux ; on peut donc dire de façon imagée " qu'elles ont tout simplement été crées ". La question du jardin d'Eden est posée pour la première fois par Moore en 1962 [Moore62], concernant les automates auto-reproducteurs. L'existence de jardins d'Eden n'a rien d'évident, car on ne voit pas a priori ce qui empêcherait une configuration donnée d'avoir un prédécesseur. En 1970, le mathématicien Alvy Ray Smith démontra l'existence de jardins d'Eden dans Life, puis un exemple fut donné par Banks. La configuration qu'il propose tient dans un rectangle de 9 par 33 cellules, cf. [Heudin98, p.62], [Poundstone85, p.50], elle est donc relativement complexe ; la démonstration elle-même est assez sophistiquée, ce qui se comprend aisément puisqu'il s'agit de montrer qu'aucune configuration de Life ne peut engendrer le candidat au titre de jardin d'Eden. Le Jeu de la Vie donne donc naissance à des problèmes qui font certes appel à l'informatique mais dont la résolution requiert des techniques purement mathématiques. D'autre part, la découverte de figures stables de plus en plus élaborées semblait montrer que malgré l'impossibilité de prévoir l'évolution de la majorité des configurations, il existait néanmoins un certain ordre dans cet univers.
Jusqu'à quel point pouvait-on maîtriser l'univers de Life ? La question fondamentale était de déterminer si Life possédait les capacités de calculabilité et constructibilité universelle. Nous avons vu que Von Neumann avait prouvé qu'un automate cellulaire pouvait servir de calculateur universel en utilisant un modèle qui employait 29 états élémentaires et dont les " lois de la physique " ne respectaient pas les conditions de symétries élémentaires telles que l'invariance par rotation et l'invariance par réflexion. Codd dans [Codd68] a fait un pas de plus vers la simplification en montrant que la condition de calculabilité universelle pouvait être réalisée par un automate cellulaire à 8 états élémentaires avec un voisinage de cinq cellules (4+1) et des règles qui respectaient l'invariance par rotation mais non l'invariance par réflexion. Jusqu'où pouvait-on continuer dans cette recherche de simplicité ? Était-il possible que Life, qui était bien plus simple dans son nombre d'états et dans ses règles puisse avoir la même puissance de calcul et de construction ? Le mystère restera entier jusqu'en 1982 où Conway publiera, avec d'autres chercheurs, une preuve détaillée de la possibilité de simuler n'importe quel calcul à l'aide du Jeu de la Vie [Berlekamp&al.82].
Dans la construction de Conway, l'unité de base qui sert à la circulation de l'information, l'équivalent d'un bit en théorie de l'information, est le planeur. Chaque nombre peut être codé selon un faisceau de planeurs généré par un lance-planeurs, et on montre que toutes les portes logiques telles que ET, OU, NON ainsi que les propriétés de mémoire en lecture / écriture peuvent être réalisées à l'aide d'interactions entre figures stables connues. Conway a aussi montré que l'on pouvait concevoir un constructeur universel dans le Jeu de la Vie. Le lecteur qui souhaiterait avoir un exposé simplifié mais qui reprend chaque étape de la démonstration de Conway peut se reporter à [Poundstone85, chap. 12]. Les constructions utilisées dans la démonstration pourront sembler étranges, complexes, voire tortueuses aux personnes habituées aux mathématiques " classiques ", mais si l'on s'y intéresse en détail on retrouve la même élégance, la même quête de l'essentiel que dans une démonstration de mathématiques. Le Jeu de la Vie allait donc apporter la preuve que la condition de calculabilité universelle peut être réalisée par un automate ayant 2 états, un voisinage de 9 cellules, et aux règles invariantes par rotation et par réflexion. A ce jour, des automates cellulaires réalisant la condition de calculabilité et de constructibilité universelle, Life est l'automate le plus simple que l'on connaisse. La démonstration de Conway allait quasiment clore le chapitre concernant le Jeu de la Vie, en effet la possibilité même de la démonstration semblait indiquer que l'on maîtrisait " suffisamment " la physique de ce monde. Il était donc temps d'explorer de nouveaux mondes.
Parallèlement aux recherches tardives qui se déroulaient sur le Jeu de la Vie, des chercheurs du MIT étudiaient d'autres automates cellulaires ayant des règles simples et qui conduisaient aussi à des comportements imprévisibles. L'un des personnages les plus marquants de cette période fut Edward Fredkin qui eut l'idée d'une règle dite de " compteur de parité " : chaque cellule compte le nombre de ces voisins activés et s'active si ce nombre est impair et se désactive si ce nombre est pair. Le compteur de parité possède une propriété remarquable : toute figure initiale s'auto reproduit en quatre ou huit exemplaires, selon que le voisinage inclut quatre ou huit cellules adjacentes. D'autres propriétés doivent être notées : (a) Le temps de reproduction dépend de la taille de la figure initiale et plus une figure est grande et plus le nombre de cycles nécessaires à l'auto-reproduction augmente. (b) Une figure donnée ne peut jamais disparaître avec le temps.
Ce compteur de parité a reçu une application dans l'industrie puisque certains ordinateurs utilisent ces propriétés pour effectuer les tests de mémoire au démarrage. En outre, le compteur de parité de Fredkin apporte un élément important dans la théorie des AC, comme contre-exemple : il est le meilleur exemple d'univers cellulaires où l'auto-reproduction est triviale puisque toute configuration initiale s'auto-reproduit !
Fredkin va former vers 1980 l'Information Mechanics Group au MIT qui inclura des noms qui deviendront célèbres dans le domaine : Tommaso Toffoli et Norman Margolus. Ce groupe de recherche a joué un rôle décisif pour exhiber les potentialités des automates cellulaires dans la résolution et la compréhension de problèmes physiques. A partir de 1984, Toffoli et Margolus ont travaillé à la construction d'ordinateurs spécialement dédiés au calcul parallèle. Leurs travaux ont abouti à la construction d'une machine appelée CAM-6 qui était un proto-ordinateur, en fait un assemblage de puces, destiné à faire tourner des modèles d'automates cellulaires. Cette machine fut perfectionnée et leur nouveau modèle, le CAM-8 fut acquis par des laboratoires américains renommés (Los Alamos, DARPA, Air Force). Toffoli, dans [Toffoli94], signale que le nombre de cellules pouvant être actualisées par seconde grimpe régulièrement et que lorsqu'il atteindra 10exp16, le nombre d'Avogadro " en deux dimensions ", les simulations seront capables de relier directement le monde microscopique et le monde macroscopique. La direction de recherche initiée par Fredkin, poursuivie par Toffoli et Margolus va se développer en une nouvelle branche dans le domaine des automates cellulaires. Cette branche s'appuie sur la thèse dite de Fredkin qui tient dans la formule lapidaire : " L'univers est un automate cellulaire ". Cette thèse ne doit pas être prise au pied de la lettre mais se veut l'analogue de la thèse de Church-Turing en informatique. Robin Gandy a d'ailleurs proposé une variante de la thèse de Church-Turing qui s'énonce sous la forme " Tout ce qui peut être calculé par une machine quelconque est effectivement calculable par une machine de Turing" dans un article où il semble prendre la " thèse de Fredkin " (en fait les travaux de von Neumann) comme base de départ [Gandy78]. La " thèse de Fredkin " conduit les chercheurs à privilégier l'utilisation des AC dans la modélisation et la compréhension des problèmes physiques.
Nous allons maintenant examiner un exemple simple - et réussi - d'automate cellulaire
modélisant des phénomènes physiques. Un aimant possède la propriété de perdre son
aimantation s'il est chauffé au-dessus d'une certaine température, appelée température
de Curie (Tc) et reprend son aimantation lorsqu'il est refroidi1. Pour expliquer ce
phénomène, on peut considérer que le matériau ferromagnétique est constitué d'un
réseau régulier de domaines (spins) qui peuvent avoir deux orientations haut et bas. On
modélise alors les interactions entre spins sous la forme suivante : un spin change son
orientation en fonction de l'orientation des spins voisins, adoptant de préférence une
configuration semblable à celle de ses voisins. La probabilité de changement
d'orientation est contrôlée par une variable aléatoire. On peut alors faire l'analogie
suivante : le changement d'orientation correspond à minimiser l'énergie (localement) et
le contrôle de la probabilité est équivalent à la température, facteur d'introduction
de " désordre " [Galam98], [Toffoli94].
La simulation montre que partant d'une configuration aléatoire, plusieurs comportements
sont possibles. Pour T>Tc, la configuration reste aléatoire. Pour T<Tc, on
s'aperçoit que des groupes se forment petit à petit jusqu'à ce qu'on distingue
clairement deux phases séparées. Le bruit thermique permet aux phases d'évoluer
jusqu'à ce que l'une d'elles finisse par dominer tout le plan. On peut même simplifier
encore le modèle d'Ising en un modèle dit 'du vote de majorité'. La règle de
transition se définit comme suit :
* Chaque cellule compte le nombre de cellules dans l'état haut et bas dans les huit cases
voisines.
* Si le nombre de voisins dans l'état haut (resp. bas) est supérieur au nombre de
cellules dans l'état bas (resp.haut), la cellule prend l'état haut (resp. bas).
* Si le nombre est égal, la cellule conserve son état.
Pour ce modèle, on observe de même une séparation des phases et une convergence très
rapide vers un état d'équilibre. De même que pour le modèle d'Ising, l'introduction de
bruit permet aux phases d'évoluer jusqu'à ce que l'une des phases recouvre tout le plan.

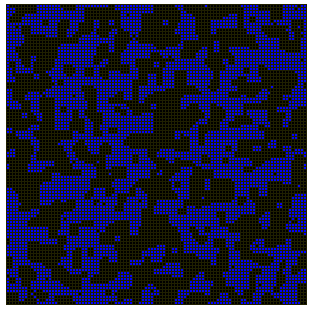

Nous avons ici choisi un exemple qui nous paraît représentatif de la puissance des AC comme outil de modélisation. Les exemples d'utilisation d'automates cellulaires pour la modélisation de phénomènes physiques sont trop nombreux pour pouvoir être énumérés. Citons comme second exemple la modélisation des milieux dits " excitables ". Ces modèles sont utilisés pour l'étude des réactions chimiques oscillantes (réactions dites de Belosov-Zhabotinsky), pour simuler la propagation des feux de forêt, ou pour simuler les opérations de réaction-diffusion [Turing52] qu'on retrouve à l'origine des formes des rayures sur les animaux. Le lecteur désireux d'en savoir plus pourra se reporter à l'excellent ouvrage de Philip Ball, The Self-Made Tapestry [Ball98]. Dans tous les cas, l'essentiel est que les modèles qu'utilisent les physiciens font tous apparaître des propriétés macroscopiques, telles que la température, la courbure des frontières entre phases et leur tension de surface à partir de la spécification, non pas d'équations, mais de règles microscopiques simples.
Les AC fournissent un exemple idéal pour étudier les propriétés d'émergence. Ces
propriétés sont généralement illustrées par la formule "le tout est plus que la
somme des parties" (1890) que l'on doit au psychologue autrichien Christian von
Ehrenfels [Bergandi2000]. On peut dire que l'émergence s'oppose au réductionnisme qui
consiste à étudier un problème le décomposant en problèmes plus petits. Cette
position épistémologique peut se lire dans les préceptes de Descartes par exemple, dans
son Discours de la méthode et on peut dire que tous les scientifiques commencent par
décomposer les entités qu'ils manipulent en entités plus petites pour essayer de
comprendre les phénomènes qu'ils étudient. Ce qui est moins clair, et ce qui divise les
savants, c'est de savoir si cette attitude suffit à résoudre les problèmes
scientifiques. On peut résumer le credo réductionniste 'naïf ' comme suit : on ne
connaîtra les lois qui règlent les sociétés qu'en étudiant les individus qui la
composent, on connaîtra les lois qui règlent les individus qu'en étudiant leur
biologie, on ne connaîtra les lois de la biologie que lorsqu'on connaîtra celles de la
chimie, etc. Les lois de la chimie elles-mêmes peuvent être déduites des lois de la
physique, le stade ultime étant que les lois de la physique peuvent se ramener aux lois
de la physique des particules. Même si cette vision des sciences interpelle, le
réductionnisme est pourtant le modèle triomphant dans la science moderne. Il est au
cœur de nombreux enjeux de société, citons par exemple celui de la psychologie :
l'étude du comportement humain doit-elle être confiée aux psychologues qui se passent
de connaissances biologiques, aux neurologues, aux spécialistes des sciences cognitives ?
Vincent Bauchau, dans un article intitulé " Emergence et réductionnisme : du Jeu de
la Vie aux sciences de la vie " écrit ainsi :
" Réductionnisme et émergence sont deux concepts liés l'un à l'autre qui sont
soit rejetés parce que triviaux, soit font l'objet de longues discussions philosophiques.
Ces deux problèmes ne sont pas seulement débattus par des philosophes, ils constituent
aussi matière à controverse au sein des scientifiques (e.g. Weinberg contre Mayr).
Comment se fait-il que les scientifiques ne peuvent pas s'accorder sur ces problèmes qui,
après tout, sont au centre de leur activité ? " [Bauchau99,
p.227].
Ce qui manque probablement pour commencer à créer un consensus, voire une théorie de l'émergence de la complexité, c'est un paradigme établi. Or, les scientifiques qui ont étudié les automates cellulaires s'accordent généralement pour déclarer " qu'ils constituent probablement les meilleurs outils pour étudier l'émergence de la complexité " [Bauchau99]. Dans le cas du Jeu de la Vie, on s'aperçoit par exemple qu'il suffit de laisser tourner une simulation initialisée aléatoirement pour voir apparaître des figures stables. On peut se demander ce qu'il adviendrait pour une simulation qu'on laisserait tourner suffisamment longtemps dans une grille très grande. Verrait-on apparaître des êtres de plus en plus évolués ? Conway n'a pas hésité à répondre par l'affirmative, en ajoutant que des organismes auto-reproducteurs apparaîtraient, évolueraient, écriraient des thèses... Aussi surprenante que soit cette idée, nous devons admettre qu'elle n'est pas plus insensée que de dire que des atomes peuvent se grouper en entités intelligentes.
Les simulations réalisées à l'aide des automates cellulaires peuvent donc nous montrer des exemples de sélection naturelle. Il existe d'autres classes de modèles où l'on voit opérer la sélection naturelle ; citons par exemple les 'algorithmes génétiques'. La différence fondamentale est que dans le cas des algorithmes génétiques, on programme le processus de sélection naturelle dans le but de trouver des solutions optimales, alors que dans le cas des automates cellulaires, la sélection naturelle n'est a priori écrite nulle part. Qui prétendrait en effet voir la moindre allusion à des objets ou à des individus dans les règles de Life (cf. I.2) ? Si nous acceptons le fait que les AC soient un modèle du monde physique, nous nous apercevons que la loi de la sélection naturelle existe alors qu'elle n'est écrite nulle part dans les lois de la physique. Nous sommes dans un cas typique d'émergence, dans lequel l'observateur voit apparaître des concepts nouveaux et des lois nouvelles, sans que ces lois ne soient déductibles à partir du niveau inférieur de description.
Néanmoins, on peut légitimement se demander si la sélection naturelle peut acquérir aussi facilement le statut de loi. En parlant de sélection naturelle, les savants écrivent : " Tout se passe comme si la nature choisissait de conserver les individus les plus aptes à survivre " [Heudin98, p. 139]. " Le tout se passe comme si " de Kant nous fait retrouver là une grande question philosophique qui est celle de savoir s'il existe une finalité dans la nature. Le débat dépasse de loin le cadre de ce mémoire, et il serait présomptueux d'affirmer que les automates cellulaires permettent de donner une réponse définitive. Néanmoins, ils constituent sans aucun doute un outil formidable pour qui veut fonder sa réflexion sur des expériences concrètes. Le débat de la finalité de la nature passionne encore les scientifiques, les épistémologues ainsi qu'un public initié, comme le témoignage d'un numéro spécial de la revue Sciences et Avenir [Sciences&Avenir2000].
L'approche par AC nous invite aussi à interroger le concept même de loi. L'idée naïve d'une loi est qu'elle est un énoncé universel qui dicte le comportement d'entités. Le Petit Larousse donne, pour le sens qui nous intéresse définit ainsi le concept de loi: " Proposition générale énonçant des rapports nécessaires et constants entre des phénomènes physiques ou entre les constituants d'un ensemble. " ; quant au Petit Robert, il énonce : " III. (1690). Formule générale énonçant une corrélation entre des phénomènes physiques, et vérifiée par l'expérience. IV. Principe essentiel et constant, condition sine qua non [...]". La majorité des épistémologues s'accorde en partie avec ces définitions et signalent que l'universalité n'est pas un critère suffisant pour attester de la validité d'une loi. Hempel donne le contre-exemple suivant : " Tous les corps purs en or massif ont une masse inférieure à 100 00 kg " [Hempel66]. Le concept de loi implique donc l'idée de nécessité, de condition sine qua non. Des épistémologues, tels que van Fraassen ont montré que cette idée de nécessité pouvait conduire à des situations inextricables ; et il va même jusqu'à préconiser l'abandon pur et simple du concept de loi pour celui de symétrie [vanFraassen89]. Ceci s'explique en partie par la constatation suivante : le monde a été créé tel qu'il est et il nous est impossible ni de changer ses conditions initiales ni de changer ses lois (si elles existent). Nous affirmons que le paradigme des AC ouvre des perspectives épistémologiques pour sortir de cette impasse en se plaçant dans contexte pluri-mondain tel que l'a pensé Leibniz : chaque automate cellulaire constituerait un univers à part entière et les lois de la physique ainsi que les conditions initiales de cet univers pourraient être décidées par l'expérimentateur. C'est d'ailleurs ce que font concrètement les chercheurs qui étudient des espaces d'AC (Wolfram, Langton, etc.) : ils décident des règles de l'automate cellulaire et initialisent le monde avec une configuration de leur choix . Dans ce contexte, des résultats surprenants sont obtenus : la sélection naturelle n'est même plus une loi fondamentale puisqu'il existe des mondes dans lesquels cette " loi " n'est pas valide. L'emploi du paradigme des AC nous conduit donc à nous interroger sur l'émergence de la complexité dans notre univers en repartant des bases même de la physique, de l'épistémologie et de la logique.
Dans les pages qui précèdent, une question omniprésente, bien que sous-jacente, a été celle de l'origine des formes. Nous l'avons rencontrée lors des discussions autour des formes auto-reproductives, des formes stables, des formes qui rappellent des phénomènes connus comme les domaines magnétiques ou les feux de forêt. Cette question se retrouve lorsqu'on cherche à comprendre les mécanismes de différentiations cellulaires : Comment en partant d'une situation constituée d'une unique cellule est-il possible de construire un individu dont les cellules sont différenciées [Turing52]?
Outre les systèmes biologiques, de nombreux systèmes physiques possèdent cette capacité de genèse des formes. L'inconvénient dans une étude physique est qu'on ne maîtrise pas toutes les données en jeu et que l'on doit sélectionner certains paramètres qu'on pense être pertinents. En cristallographie par exemple, si l'on observe que des atomes s'organisent en un réseau cristallin, on explique ce phénomène en termes de nuages électroniques et d'énergie du système. Les atomes sont considérés comme des sphères isotropes et on ne fait jamais appel à une quelconque forme des atomes pour expliquer la forme du réseau. Pourtant, le doute est permis : et si les atomes avaient réellement une forme et si c'était leur forme qui expliquait celle du réseau ? Cette hypothèse est bien entendu fantaisiste mais elle a le mérite de montrer que dans toute expérience faisant intervenir des entités physiques, l'explication de l'émergence d'une forme peut donner lieu à controverse. Citons par exemple les travaux de Turing relatifs à la morphogenèse [Turing52] : les substances morphogénétiques introduites étaient une pure spéculation, un moyen mathématique pour expliquer la différenciation cellulaire. Très longtemps, le doute a plané sur la réalité de ces substances et ce n'est qu'à l'aide de travaux récents que l'on a réussi à montrer l'existence de mécanismes analogues à ceux décrits par Turing.
L'utilisation des AC permet d'éviter qu'il y ait le moindre doute quant à l'origine des formes : avec les AC le concepteur de l'automate a toutes les données en main. Il ne peut donc pas justifier son ignorance sur l'origine des formes qu'il observe en prétendant qu'il ne possède qu'une connaissance imparfaite de son système : chaque donnée peut être connue de lui. La question de l'origine des formes et de l'évaluation de leur complexité est très vaste, elle peut être traitée sous de nombreux angles. Un paramètre qui nous semble important à étudier dans la théorie des AC est la capacité d'un automate à faire apparaître des formes En se fondant sur les travaux précédemment examinés, notamment [Toffoli94] et [Bauchau99], nous pensons que l'utilisation des AC pourra apporter de nombreux éclaircissements à cette question, notamment à l'aide de l'étude des variations de l'entropie des systèmes avec le temps.
Cet exposé nous a permis de retracer l'histoire des automates cellulaires, depuis leur invention dans les années 50 jusqu'aux recherches plus récentes. Tout d'abord conçus pour répondre à un problème bien spécifique, celui de la construction d'un automate auto-reproducteur, les AC ont été un prétexte à un grand mouvement de recherche initié avec le Jeu de la Vie. Ils se sont ensuite en quelque sorte " émancipés " et leur intérêt comme classe de modèles s'est fait ressentir dans un grand nombre de domaines scientifiques allant de la physique aux sciences humaines, gagnant par-là le statut de paradigme scientifique. L'histoire des automates cellulaires part donc de l'étude d'un AC particulier dédié à un but articulier (von Neumann, Codd), se développe lors de l'étude d'un AC conçu comme un jeu (Conway), puis se généralise comme classe de modèles (Wolfram, Langton, etc.). L'histoire des AC suit donc un mouvement de généralisation croissante jusqu'à la constitution d'un paradigme. Néanmoins, les utilisateurs des automates cellulaires restent des précurseurs et force est de reconnaître que leur usage ne s'est pas encore répandu dans les milieux scientifiques et industriels. Faire appel à un automate cellulaire pour résoudre un problème scientifique ne va pas de soi.
La raison probable de cet engouement relativement faible des chercheurs pour leur utilisation est la difficulté que nous avons dans la compréhension des phénomènes impliquant le parallélisme. Nous sommes généralement désarmés lorsque nous devons construire un modèle qui prédit l'évolution de nombreux paramètres dans l'espace et le temps. Comme le signale un chercheur qui utilise les automates cellulaires dans la modélisation de la dynamique urbaine, les premiers modèles de peuplement en géographie se concentraient sur des données telles que la population, la densité et, comble du paradoxe, oubliaient la répartition dans l'espace proprement dite [Langlois97]. L'élaboration d'une théorie des automates cellulaires est donc un enjeu scientifique majeur pour la compréhension de tous les phénomènes dans lesquels le parallélisme est une caractéristique fondamentale ; et à bien y regarder, on s'aperçoit qu'il s'agit de la majorité des phénomènes.
L'enjeu n'est d'ailleurs pas seulement scientifique mais aussi technique : au XXIe siècle l'environnement semble se modeler à l'image des réseaux et il est probable que les résultats théoriques obtenus avec les AC pourront influencer considérablement l'état des techniques. Une condition nécessaire à l'explosion des AC est la maîtrise des architectures d'ordinateurs parallèles : à quoi bon en effet simuler le fonctionnement d'une machine parallèle sur une machine séquentielle ?
Un autre trait remarquable de cet outil est que malgré son aspect fondamentalement mécanique (c'est l'aspect automate), les chercheurs qui étudient les univers cellulaires ont une attitude de naturalistes : la recherche de régularités se fait essentiellement à l'aide de l'observation (c'est l'aspect cellulaire). Pourtant, dans une construction qui est faite avec un automate cellulaire, tout est maîtrisé, du moins dans la situation initiale. On pourrait donc penser que la maîtrise du déroulement d'un AC conduit à faire des expériences ennuyeuses où tout ou presque peut être prévu d'avance. En vérité on s'aperçoit que c'est tout le contraire. Nous avons vu que des règles aussi simples que celles de Life peuvent conduire à des comportements imprévisibles et inattendus. Aussi, l'étonnement surgit pour toute personne qui regarde évoluer un automate cellulaire non trivial. Pour celui qui programme Life, le modèle d'Ising ou celui des feux de forêt, la question : " Comment est-ce possible de capter un comportement aussi riche en utilisant si peu de lignes de programmation ? " surgira immanquablement. Qu'il s'agisse de définir ce qu'est la vie, de comprendre l'origine de la complexité de l'univers ou de mieux cerner la notion de loi de la nature, nous avons vu que les AC par leur aspect minimaliste nous obligent à aller au fond des problèmes : leur utilisation invite au questionnement philosophique. Il nous semble donc probable que les automates cellulaires retiendront une part grandissante de l'intérêt des philosophes des sciences. Nous pensons que les automates cellulaires sont un domaine de recherche d'avenir, qui n'a encore livré que quelques secrets. Idéalement, l'étude des automates cellulaires conduira autant à mieux comprendre les phénomènes qu'à s'interroger sur la façon dont nous comprenons ces phénomènes ; il est donc probable que cette classe de modèles abstraits serve de lien entre scientifiques et épistémologues. L'étude des automates cellulaires peut être ramenée dans un cadre plus vaste, celui des sciences dites de " la complexité ", qui incluent l'étude des systèmes dynamiques chaotiques, la théorie de la morphogenèse, la vie artificielle, etc. Chacun de ces domaines possède ses propres paradigmes et les connexions entre eux restent très faibles. Nous pouvons dire que le seul lien fondamental entre les disciplines des sciences de la complexité est d'utiliser l'ordinateur comme outil fondamental Il n'y là apparemment rien d'extraordinaire mais nous pouvons sentir un changement radical dans la vision de la science : alors que les savants s'interrogent depuis l'antiquité si le monde est écrit en langage mathématique, un nouvel enjeu philosophique tend à émerger : celui de savoir si le monde est écrit en langage algorithmique. A Leibniz, qui en marge d'un dialogue écrit en 1677 : Cum Deus calculat et cogitationem exercet, fit mundus : " Tandis que Dieu calcule et exerce sa cogitation, le monde se fait. " ; nous sommes désormais tentés de dire : " Tandis que Dieu calcule (effectue) des algorithmes et exerce sa cogitation, le monde se fait " .
Ecrire à l'auteur :
* par Email: FatesNazim@aol.com
* par couurier : Nazim Fatès 18, rue Solferino F-92 170 Vanves
[Ball98] P. Ball, The Self-Made Tapestry, Oxford University Press, 1998.
[Bauchau99] V. Bauchau, « Emergence et réductionnisme : du Jeu de la Vie aux sciences de la vie » in Auto-Organisation et émergence dans les sciences de la vie, sous la dir. de B. Feltz et al., Editions OUSIA, distribution à Paris : Vrin, 1999.
[Bergandi2000] D. Bergandi, « L’idée d’émergence », in Sciences et Avenir Hors-Série Les grandes idées du siècle, Janvier 2000.
[Buffon] Comte de Buffon, De la manière d’étudier et de traiter l’histoire naturelle - Oeuvres Complètes, 1774-1779.
[Codd68] E. F. Codd, Cellular Automata, New York Academic Press, 1968.
[Culik88] K. Culik, S. Yu, “Undecidability of CA classification schemes”, Complex Systems, 2, p.177, 1988.
[Berlekamp&Al.82] E. Berlekamp, J. Conway, G. Richard, Winning ways, vol. 2 , New York : Academic Press, chap. 25, 1982.
[Galam98] S. Galam, « Sous les chemises... La symétrie » in Dossier Pour la Science - Les symétries de la nature, Juillet 1998.
[Gandy78] R. Gandy, “Church's thesis and principles for mechanisms” (1978), The Kleene Symposium, Edité par J. Barwise& al,. North-Holland Publishing Co., Amsterdam-New York, 1980.
[Gardner70] M. Gardner, "Mathematical Games: The fantastic combinations of John Conway's new solitaire game ‘life’", Scientific American, pp. 120-123, Octobre1970.
[Goujon99] Ph. Goujon,“De la logique à l’auto-organisation”, » in Auto-Organisation et émergence dans les sciences de la vie, sous la dir. de B. Feltz et al., Editions OUSIA, distribution à Paris : Vrin, 1999.
[Hempel66] C. Hempel, Eléments d’épistémologie (1966), Paris: Armand Colin / Masson, 1996.
[Heudin97] J-C. Heudin, M. Magnier, C. Lattaud, « Complexity classes in the Two-dimensional Life Cellular Automata Subspace », Complex Systems, N° 11, pp.419-436, 1997.
[Heudin98] J-C. Heudin, L’évolution au bord du chaos, Paris : Hermès, 1998.
[Kant] E. Kant, Critique de la Raison Pure (1781), Paris : PUF/Quadrige, 1997.
[Kuhn70] T. Kuhn, La structure des révolutions scientifiques (1970), Flammarion, 1983.
[Langton84] C. G. Langton, “Self-Reproduction in Cellular Automata”, Physica D, n°10, pp. 135-144, 1984.
[Langlois97] A. Langlois, M. Phipps, Automates Cellulaires - Application à la simulation urbaine, Paris : Hermès, 1997.
[Langton90] C.G. Langton, “Computation at the edge of chaos : phase transition and emergent computation”, Physica D 42, pp. 12-37, 1990.
[Leibniz] G.W. Leibniz, Oeuvres, édition Gerhardt, Berlin 1875-1890, tome VII, p.191 cité in Gérard Chazal, Formes, Figures, Réalités, Champ Vallon, 1997.
[Moore62] E. Moore, “Machine models of self-reproduction.” in Proc. Symposia Applied Mathematics, Vol. XIV, Amer. Math. Soc. , pp.17-34, 1962.
[Moore64] E. Moore, Sequential Machines, Selected Papers, Addison Wesley, 1964.
[Odifreddi89] P. Odifreddi, Classical Recursion Theory, North-Holland, 1989.
[Poundstone85] W. Poundstone, The Recursive Universe, Oxford University Press, 1985.
[Sciences&Avenir2000] Sciences et Avenir, Hors-Série : « La finalité dans les sciences, Le sens de la vie », Octobre-Novembre 2000.
[Time74] “The Game of Life”, Time, 21 Janvier 1974.
[Toffoli94] T. Toffoli, “Occam, Turing, von Neumann, Jaynes: How much you can get for how little ? ( A conceptual introduction to cellular automata )”, InterJournal, Décembre 1994.
[Turing36] A.M Turing, “On Computable Numbers, with an application to the Entscheidungsproblem”, Proceedings of the Mathematical Society, Série 2, Vol. 42 (1936-1937), p.230-265.
[Turing52] A.M Turing, “The chemical basis of morphogenesis”, Philosophical Transactions of the Royal Society, N° 237, 1952.
[Turing54] A.M Turing, “Solvable and unsolvable problems”, Science news 31, 1954.
réimp. in Collected works, Pure mathematics, pp. 99-115, 261-263.
[Ulam50] S. Ulam, "Random Processes and Transformations", in: S. Ulam, Sets, Numbers and Universes, Cambridge : MIT Press , pp. 326-337, 1974.
[vanFraassen89] Bas C. Van Fraassen, Lois et Symétries (1989), Paris : Vrin, 1994.
[vonNeumann66] John von Neumann, Theory of Self-Reproducing Automata, Urbana : University of Illinois Press, 1966.
[Wolfram83] S. Wolfram, « Statistical Mechanics of Cellular Automata » in Review of Modern Physics 55, pp.601-644, 1983.
[Yunes93] J.B. Yunès, Synchronisation et automates cellulaires : la ligne de fusilliers, Thèse présentée à l’université Paris 7, 17 février 1993.